Special Topic

ARTICLE: Why the moon always shows us the same face

by Alain Dondelinger

If you have ever observed the Moon over an extended period (say a month...), you may have noticed that the moon always shows us the same face. Maybe you have asked yourself why it does not seem to rotate, as do the other celestial bodies, like Mars, Jupiter. Before you continue reading, you should know that this was not always the case, i.e. the Moon once was rotating with respect to the Earth, so that on every night a terrestrial observer (if there was one, because this was long, long before mankind appeared on our planet, and even before any major animals had appeared) saw another face of the Moon.
We are unable to find an answer to this question without making a small excursion to newtonian physics; but don’t worry it’s not as hard as you might think when you hear “physics”.

Newton’s Law of Universal Gravitation

In the 17th century, Isaac Newton, a well known English physicist published his Law of Universal Gravitation. In short, this law states that the force acting between two massive bodies (bodies which have a mass) increases with the masses of the interacting bodies, and that it decreases with the distance separing the two bodies. This law which takes a quite simple form in mathematical terms, allows us to make some quite interesting predictions about the movement of the interacting bodies (I won’t give more details here, if you want to investigate this subject further, you may find good documentation in any elementary textbook about classical mecanics. Unfortunately this requires some knowledge in maths and secondary school or undergraduate physics).

Newton’s Universal Law of Gravitation explains why and how Earth (or any other planet) orbits around the Sun or the Moon around Earth. Figure 1 (not to scale) shows how we can imagine the system Earth-Moon. The force (F) “pulling” Earth has the same intensity as the force “pulling” the Moon. As the Moon is much less heavier than the Earth is, it is finally the Moon that “runs” around the Earth (with the velocity (v), which we can calculate by using Newtons Law of Gravitation and a few other laws of classical mechanics) and not the Earth that runs around the “Moon”.


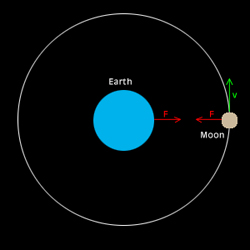
fig.1

This law of universal gravitation is quite easy to manipulate. This is mainly due to the fact that, in a first approximation, you can assume that the interacting bodies are like massive points, i.e. all the mass of one body is confined into a very small space.

Tidal forces

If the two interacting bodies described in the previous paragraph are quite big, as are the Earth or the Moon, and if you want to investigate the problem of the Moon’s movement a bit further, you may not consider those celestial bodies as massive points. This has a very important consequence: as depicted in figure 2, different places on Earth do feel different forces (different both in direction and intensity). This is because those places are not at exactly the same distance from the Moon. Of course this is also true for different locations on the Moon, because they are at different distances from Earth.

This differences of the forces explain the effect we commonly know as “tides”. This effect is most important for liquids, e.g. the water forming the oceans on our planet. But it does also exist for the continents, even if it is less important in that case. And, as you may guess, the same applies to the Moon. This results in a somehow “eggshaped” Moon and Earth, the difference from a sphere being so small that it may only be detected with very sophisticated experiments.


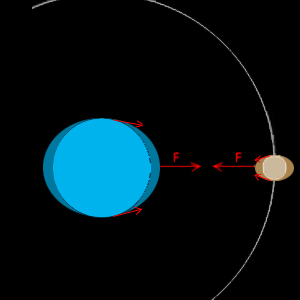
fig.2

Please note that the tides are largely exagerated on this figure!

Why the moon always shows us the same face

Now, here finally comes the explanation to the question asked in the beginning. As soon as a body has some mass, it also has a property called inertia. This property makes that the body does not react immediately to the force applied upon it, or in other terms that it is difficult to change the movement of a massive body. A consequence of this is that at a given location (on Earth) the tides do not appear at the exact moment when the moon is “facing” it, but a bit later (minutes or hours). Again, the same is true for the Moon. The “egg” (somehow allongated Moon) is not aligned with the line Earth-Moon, but makes a small angle with it, as shows figure 3.




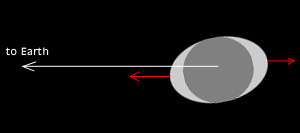
fig.3

If this happens, there appears a couple of forces, trying to align the Moon again with the Earth-Moon-line. Now remember what I told you in the very first paragraph of this short article: in a very far past the Moon seemed to rotate when observed from the Earth. The effect of the couple of forces was to slow down this rotation, so that eventually the rotation of the Moon “came to rest” for a terrestrial observer…

Well, this is why the Moon actually always shows us the same face!

In order to better understand the phenomenon at work here, try the following (very simple) experience:
From a cardboard, cut a “Moon” that has roughly the shape of the one depicted in figure 3. At the places of the red arrows, attach a piece of (sewing) thread. If you put all this like the Moon in figure 3 and try to pull on the threads in direction of the red arrows, you will notice that your cardboard-moon rotates until its longest axis is parallel to the direction in which you pulled.

About the Author - Alain Dondelinger

Language may vary from the one used in the article.

Alain is studying for a Master's Degree in Physics at the Université Louis Pasteur (Strasbourg, France). Unfortunately work for school consumes most of his time, which leaves him only few time for astrophotography, the part of amateur astronomy that interests him most. He is member of AAL since 1993

SPECIAL TOPICS HISTORY
Period	Subject Author	Language	Available Formats
June 2023	h-alpha Solar pictures using minimal means error	EN	PDF=7442.8kB
October 2021	Starting out with Astrophotography	EN	PDF=7709.4kB
May 2008	De Summerstärenhimmel	LU	PDF=2005.7kB
September 2006	Ein aussergewöhnlicher Abend mit John Dobson in Saarlouis	DE
April 2006	Total Solar Eclipse 2006	LU
May 2004	Venus Transit 2004	EN
April/May 2002	Die Roche’sche Grenze	DE
Apr/May 2001	Das Foucault'sche Pendelexperiment	DE
Feb/Mar 2001	The Hertzsprung-Russell Diagram	EN	PDF=827.2kB
Jan 2001	Die Jagd nach Exo-Planeten	EN	PDF=544.4kB
Sep/Oct 2000	Entdecker des Sonnensystems	EN
Jun/Jul 2000	Comet Linear Special	EN
Apr/May 2000	The Adventurous Search For The Astronomical Unit	EN
Mar 2000	Why the moon always shows us the same face	EN

Get Acrobat Reader!